當制造的構件為傳動部件,并且工作面在加工中承受高頻動態應力時,表面完整性問題尤為重要。面齒輪表面完整性的主要特征之一為殘余應力,因其影響著齒面的抗疲勞特性,對面齒輪系統的服役性能和使用壽命,具有重要的影響作用。殘余應力解析建模的實質是將加載過程邊界條件被破壞的情況進行卸載,以恢復邊界條件。
在恢復邊界條件的過程中,產生的新的應力即為殘余應力。賈東洲等首先分析了靜電霧化微量潤滑粒徑分布特性,通過使用微量潤滑劑使得摩擦因數減小了 9.31%~29.39%,有效改變鈦合金材料的磨削性能。黃保騰等采用 WA 和 SG 砂輪磨削鎳基合金 GH4169,從磨削力、工件表面形貌、磨削比能 3 個方面評價兩種砂輪的磨削性能,并探究磨削參數對砂輪磨削力、工件表面形貌、磨削比能的影響規律。
結果表明 SG 砂輪具有優越的抗磨性能,可以獲得良好的工件表面質量。在后續研究中,通過添加生物潤滑劑研究磨削能、比磨削力、表面粗糙度和磨削溫度的變化規律。
針對平面淬硬磨削加工,張靜發現了磨削接觸區域的熱應力為壓應力;當砂輪移開加工區域后,熱應力由壓應力迅速轉變為拉應力。同時指出,在淬硬磨削中,相較于機械應力,熱應力對殘余應力 的貢獻更大。
針對小切深磨削,張曉曉等建立了機械應力解析模型,分析了磨削接觸區域沿砂輪進給方向的機械應力分布,結果表明,機械應力在砂輪切入點表現為拉應力,在磨削接觸弧長內也表現為拉應力,并呈現先增大后減小的變化趨勢,在砂輪切出點表現為壓應力;同時指出,在小切深磨削加工中,機械應力的作用深度有限。
Zhao B 等在超聲輔助磨削漸開線齒輪的應力分析中發現,機械載荷在的 Y 向和 Z 向的正應力為壓應力,在 Y-Z 平面上的切應力上也是壓應力。張子輿建立了針對鋼軌打磨的三維仿真模型,結果發現,Mise 應力與砂輪轉速呈負相關,與砂輪轉速呈正相關。針對硬質合金 GT35 材料的平面磨削,付天章等研究了平面磨削 GT35 殘余應力的形成機理,分析了平面磨削加工工藝參數對表面殘余應力的影響,實現了低殘余應力加工的可控工藝方案。針對螺旋傘齒輪的展成磨削,北京理工大學梁志強教授等采用有限元法實現了綜合力-熱耦合的齒面殘余應力分析,結果表明,齒面殘余應力與砂輪線速度呈負相關,與展成速度呈正相關。
在面齒輪的展成磨削過程中,砂輪與工件之間的相對運動影響齒輪的磨削效率和齒面質量,而磨削過程中的力、熱改變會引起殘余應力分布發生變化,從而改變面齒輪的接觸強度、抗彎強度和抗疲勞強度等性能指標,影響面齒輪的服役性能和服役壽命。面齒輪展成磨削表面殘余應力優化是一個復雜的非線性問題,傳統的優化算法無法實現高效率和高精度的求解。因此,需要采用智能優化算法獲得問題的最優解。本文以砂輪速度、工件速度、磨削深度和砂輪分度角 4 個工藝參數為優化變量,以面齒輪的齒面殘余應力為優化目標,使用粒子群優化算法(particle swarm optimization,PSO),解決了面齒輪表面殘余應力的優化問題。
一、磨削參數優化組合設計
針對面齒輪展成磨削,將較大且齒面分布均勻的殘余壓應力,以及較高的磨削效率作為優化目標。優化變量包括砂輪速度、工件速度、磨削深度和砂輪分度角等工藝參數,其邊界條件的確定依據和數值區間如下:
(1)針對磨削深度,其數值過大會導致磨削力增大、磨削溫度升高和表面形貌變差等;而數值過小會導致磨削效率降低、殘余壓應力較小等。除此之外,砂輪的磨粒大小也是限制磨削深度的重要因素,在本文中,砂輪磨粒目數為 200 目。根據以上條件,磨削深度的邊界條件為 0.01~0.05 mm。
(2)針對砂輪速度,其數值過高會導致砂輪磨粒過早失效、砂輪壽命降低、表面氧化加劇等。砂輪速度過低會導致切屑厚度增加、磨削淬硬概率增大、表面粗糙度變優等。針對面齒輪展成磨削,根據 Wang Y Z 等的研究,砂輪速度的邊界條件為 20~60 m/s。
(3)針對工件進給速度,其數值過高會導致接觸時間縮短、接觸長度減小、表面精度降低等問題。工件進給速度過低會導致接觸時間延長、接觸長度增大、表面溫升過高、表面氧化加劇等問題。針對面齒輪展成磨削,將工件進給速度的邊界條件設置為 0.5~3 m/min。
(4)針對砂輪分度角,其數值過大使得面齒輪展成磨削的齒面材料去除率較低,導致齒面殘差過大,從而影響齒面的加工質量和表面粗糙度。砂輪分度角過小,會引起砂輪的空走刀,降低磨削效 率。針對面齒輪展成磨削,根據郭輝等的研究,當砂輪分度角在 0.2°~ 0.5°時,可以滿足齒輪六級精度的包絡殘差加工要求。
針對面齒輪的表面殘余應力的研究,發現齒面不同位置(齒頂、齒中和齒根)的表面殘余應力具有明顯的差異。因此,將齒面的磨削位置作為附加的優化變量。
綜上,考慮齒面的磨削位置,磨削深度的邊界條件為 0.01~ 0.05 mm,砂輪速度的邊界條件為 20~ 60 m/s,工件進給速度的邊界條件為 0.5~ 3 m/min,以及砂輪分度角的邊界條件為 0.2°~0.5°, 采用 Box-Behnken 的方法設計磨削工藝參數的優化組合。為 Box-Behnken 方法的因素和水平,見表 1。
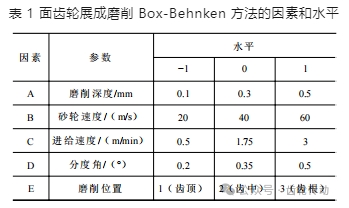
二、表面完整性模型驅動的優化目標響應曲面建模
根據磨削工藝參數的 Box-Behnken 實驗組合,通過面齒輪磨削試驗,獲得了對應的齒面殘余應力,形成相應的響應曲面模型。考慮殘余應力的區域性分布特點,優化目標要求齒頂、齒中和齒根 3 個區域之間的殘余應力數值相近,形成齒面均勻的齒面殘余應力狀態。此外,磨削效率的評價標準是磨削時間。
齒面殘余應力獲取實驗
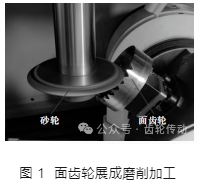
根據 Box-Behnken 實驗組合,在 V33-5XB 牧野加工中心對面齒輪進行磨削,如圖 1 所示。已知面齒輪的材料為調質后的 45#鋼,在機加工前對材料做去應力退火處理。加工工藝完成后,采用線切割工藝切斷輪齒,并在 HDS-X 射線應力儀獲得了齒面殘余應力。
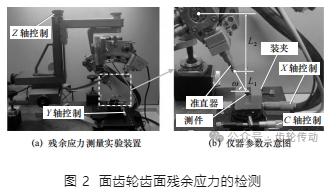
在檢測過程中采用準直管的光孔直徑為 2 mm,測量前設置測量條件,包括測量方法為側傾固定 ψ 法,選擇 ψ 為 0°和 45°,并用 Cr-Kα 射線測定鐵素體(211)晶面(θ=156°)的衍射峰。在測量過程中,X 射線通過一個光孔輻照在工件表面的局部區域,測量得到局部區域的殘余應力,面齒輪齒面殘余應力的檢測,如圖 2 所示。根據參考文獻,X 射線的輻照區域為一橢圓區域,橢圓的短 軸和長軸分別為 dx 和 dy,檢測得到的殘余應力數值可以看作輻射面積的平均值。dx 和 dy 的求解公式為
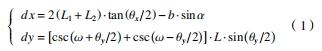
式中:L1、L2 和 L 的取值分別為 120、85 和 149;b表示焦點的尺寸參數,取值為 0.5 mm;α 表示 y 焦點的傾斜角,取值為 6°;θx 和 θy 表示扇角,取值均為 0.05°;表示 y 方向的入射角,由側傾固定 ψ 法的測量特點,得到的數值分別為 57°和 79°,部分參數示意圖如圖 2b 所示。
齒面殘余應力的響應曲面模型
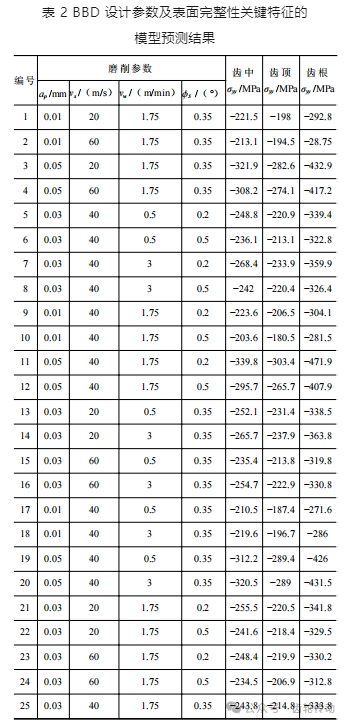
使用 Design Expert 統計軟件創建了 Box-Behnen Design(BBD)優化組合,見表 2,得到了磨削深度、砂輪速度、工作速度和砂輪分度角與殘余應力之間的關系。由于 x 方向與 y 方向的殘余應力具有相同分布特征,因此,只需建立 y 方向齒面殘余應力的二次響應面模型即可。
通過統計軟件分析,得到了齒面中部區域 y 方向齒面殘余應力的響應曲面方程:
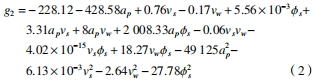
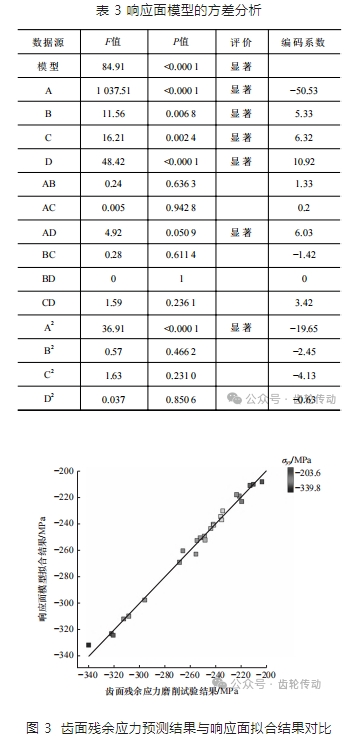
響應曲面模型的檢驗結果,見表 3。根據方差分析,響應面模型的 F 值為 84.91,P 值遠小于 0.05,說明該模型有很高的置信水平。模型的 R2 為 0.991 7,表明模型具有較好的擬合效果。齒面殘余應力預測與響應面擬合的結果對比如圖 3 所示。
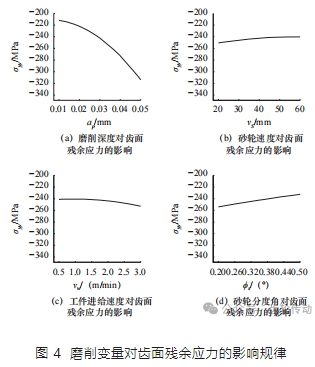
為了評價各因素對齒面殘余應力的影響規律,繪制了主效應圖,如圖 4 所示,分別顯示了磨削深度、砂輪速度、工件速度和砂輪分度角對齒面殘余應力的影響規律及敏感性。結果表明,齒面殘余壓應力與磨削深度和工件速度呈正相關,與砂輪速度和砂輪分度角呈負相關。從敏感性角度分析,齒面殘余應力對磨削深度的敏感性最大,其次是砂輪分度角,而齒面殘余應力對砂輪速度和工件速度的敏感性相對較小。磨削工藝參數對齒面殘余應力的作用機制如下。
(1)隨著磨削深度的增大,齒面殘余壓應力增大。這是由于隨著磨削深度的增大,單顆磨粒的未變形切屑厚度增大,磨削力增大,磨粒對齒面表層的擠壓力增大,機械應力增大。根據面齒輪展成 磨削的加工特點,以及較小的磨削深度(小于 0.05 mm),使得參與磨削的砂輪磨粒較少。由面齒輪磨削溫度場模型可知,較少的磨粒以及較小的切深,決定了面齒輪的磨削溫度較低,導致齒面熱 應力較小。對比齒面熱應力,齒面機械應力占據主導地位。根據機械殘余應力和熱殘余應力的疊加效應,可知齒面殘余壓應力增大。
(2)隨著砂輪速度的增大,齒面殘余壓應力減小。這是由于隨著砂輪速度增加,單位時間內參與磨削的磨粒數量增多,單顆粒的未變形切屑厚度減小,磨削力減小,機械應力減小。然而,處于滑 擦和犁耕階段的磨粒數量增加,摩擦產熱增多,磨削溫度升高,齒面熱應力隨之增大。根據機械殘余應力和熱殘余應力的疊加效應,可知齒面殘余壓應力減小。
(3)隨著工件速度的增加,齒面殘余壓應力增大。這是由于隨著工件速度的增加,單顆磨粒的未變形切屑厚度增大,磨削力增大,磨粒對齒面表層的擠壓力增大,機械應力增大。而磨削接觸區域 與工件的接觸時間變短,傳遞到工件的磨削熱減少, 齒面溫度降低,熱應力隨之減小。根據機械殘余應力和熱殘余應力的疊加效應,可知齒面殘余壓應力增大。
(4)隨著砂輪分度角的增大,齒面殘余壓應力減小。這是由于隨著砂輪分度角的增大,參與齒面磨削的磨粒數量增多,根據面齒輪磨削溫度場模型可知,較多的磨粒熱源提高了磨削溫度,齒面熱 應力隨之增加。而單顆磨粒的磨削力并未變化,機械應力并未顯著改變。根據機械殘余應力和熱殘余應力的疊加效應,可知齒面殘余壓應力減小。
同理,在 Design Expert 統計軟件內分別得到了齒面頂部區域和齒面根部區域的齒面殘余應力的響應曲面模型,分別用 g1 和 g3 表示:

g1 和 g3 的 P 值均小于 0.000 1,R2 分別為 0.978 0 和 0.983 2,證明了響應曲面模型的有效性。
基于粒子群智能算法的多目標優化
PSO 是一種基于群體智能的優化算法,靈感來源于鳥群、魚群等生物群體的行為。PSO 通過模擬群體中個體的社會行為和個體之間的合作,以尋找問題的最優解。PSO 的基本原理是通過模擬粒子在解空間中的移動來尋找最優解。在 PSO 中,每個粒子代表一個潛在的解,它在解空間中搜索,并根據自己的歷史經驗和群體的經驗進行位置的更新。每個粒子都有一個位置和速度,根據其個體最優解和群體最優解進行調整,從而逐漸收斂到最優解附近。PSO 的算法流程,如圖 5 所示。PSO 具有全局搜索能力強、自適應性強、并行性強、簡單且易實現,以及不易陷入局部極值等優勢,廣泛應用于目標優化問題。
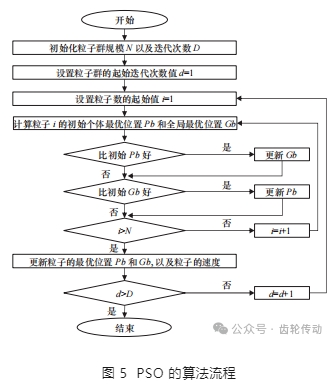
根據建立的齒面殘余應力響應曲面模型,以最大殘余壓應力和齒面均勻的殘余壓應力,以及較高的加工效率作為優化目標,對面齒輪展成磨削工藝參數進行多目標優化。為了降低優化目標的復雜性,將面齒輪的齒面分為齒頂、齒中和齒面 3 個部分,再分別求解優化工藝參數。同時,需要增加殘余壓應力的約束條件,即整個齒面的殘余壓應力約束在 −300 MPa<gi<−280 p="" 3。優化目標可以表示為<="" 2,="" i="1," mpa,其中=""> </gi<−280>
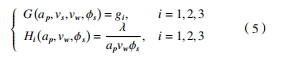
式中:λ 表示常數,可根據齒面材料余量、齒輪寬度和齒輪展成總角度確定。約束條件可以表示為

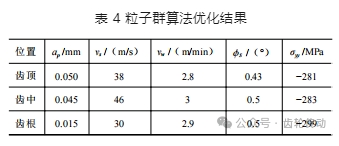
通過粒子群優化算法,得到了齒頂、齒中和齒根區域的磨削工藝參數及對應的齒面殘余應力,見表 4。
三、面齒輪表面殘余應力的優化方法驗證
在齒面殘余應力檢測過程中,采用準直管的光孔直徑為 2 mm,在齒面、齒中和齒根區域分別選取一處測量位置,測量 3 次后取平均得到了齒面 y 方向和 x 方向的殘余應力,如圖 6 所示。由圖可知,齒頂、齒中和齒根區域的 y 方向殘余應力分別為 −278.5、−289.6、−303.8 MPa。對比表 4 中結果,相對誤差分別為 0.89%、2.33%、1.61%。
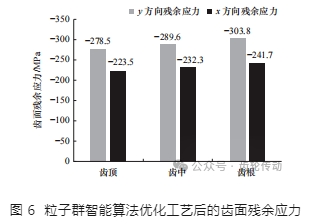
由測量結果可知,優化后的齒面 y 方向的殘余應力介于−303.8~−278.5 MPa,齒面 x 方向的殘余應力介于−241.7~−223.5 MPa,有效提高了齒面殘余應力的分布均衡性,實現了對面齒輪表面完整性關鍵特征的優化調控。同時,磨削機動時間縮短 14% 以上,有效提高了加工效率。
四、結語
本文提出了以齒面磨削實驗數據為數據驅動的面齒輪表面殘余應力優化方法。以磨削工藝參數為優化變量,以獲取需要的齒面殘余應力和較高的磨削效率為優化目標,解決了面齒輪表面殘余應力的優化問題。根據本文的研究內容,可以得到如下結論:
(1)齒面殘余壓應力與磨削深度和工件速度呈正相關,與砂輪速度和砂輪分度角呈負相關。從敏感性角度分析,齒面殘余應力對磨削深度的敏感性最大,其次是砂輪分度角,而齒面殘余應力對砂輪速度和工件速度的敏感性相對較小。
(2)使用粒子群智能優化算法,獲得了齒面均勻且表面殘余應力約束在−300 MPa<σyy< −280 MPa 范圍內的磨削工藝參數,而實際測量值為−278.5 MPa <σyy<−303.8 MPa。對比結果表明,基于粒子群智能算法的多目標優化模型的相對誤差介于 0.89%~1.61%,證明了面齒輪展成磨削表面殘余應力優化方法的有效性。
參考文獻略.
