齒輪是航空傳動系統最重要的結構件之一,工作環境十分復雜。齒輪材料性能決定了齒輪的核心性能,整個航空減速器的質量、承載能力、干運轉能力、壽命等核心指標均與之密切相關。隨著航空發動機的不斷更新發展,對齒輪承載能力和使用溫度提出了更高的要求,要求齒輪鋼具有優良的強度和疲勞特性。
目前國際上航空齒輪主要以 9310 鋼、EX ?53(AMS 6308)鋼、15Cr14Co12Mo5Ni2WA 鋼為代表的第一、二、三代航空齒輪鋼。其中,第二代齒 輪鋼 EX ?53(AMS 6308)相對于 9310 鋼,具有更高溫度下的組織穩定性和抗高溫應力松弛能力,可以承受比 9310 鋼更高的服役環境。第三代齒輪鋼,是一種具有強韌性、耐高溫、耐腐蝕、耐磨損性能和疲勞強度的新一代航空齒輪鋼,其材料性能指標相對 9310 鋼和 EX ?53 鋼有較大的優勢。但是由于對這種材料缺乏應用研究,目前還未掌握其應用在齒輪上的彎曲疲勞極限和 R ?S? N(可靠?應力?壽命)等重要材料性能,成為制約該材料在齒輪傳動系統的應用的瓶頸,輪齒的疲勞失效是十分常見的突出問題,急需得到該材料齒輪的彎曲疲勞極限和 R?S?N,保證設計的安全性。
疲勞失效通常指材料、構件或零件在循環應力或循環應變作用下,經過一段時間后突然斷裂的現象。據統計,機械零件的破壞 50%~90% 為疲勞失效。為解決上述問題,國內外學者針對齒輪疲勞強度分析及其影響因素開展了大量的理論研究工作。對于航空齒輪而言,彎曲疲勞強度是衡量其傳動性能的重要指標,是保障整個機構安全的關鍵。
何曉華針對 20CrMoH 齒輪的彎曲疲勞強度進行了分析和研究,得到了該材料的不同存活率下的疲勞壽命(P?S?N)曲線曲線,陳毅和馬騁天等對 20CrMnMo 材料的齒輪的彎曲性能、齒根彎曲應力進行了測試;李銘等在恒定應力水平下進行齒輪彎曲疲勞試驗,獲得了 20CrMn? Ti 滲碳齒輪的彎曲疲勞壽命數據。
Benedetti 等針對表面硬化的 16MnCr5 鋼齒輪進行了彎曲疲勞試驗,分析了該材料齒輪的發生斷了的原因。Peng 等針對 9310 鋼采用單齒彎曲法進行了疲勞試驗,對比了激光強化對齒輪的影響。趙文杰等針對用于高鐵使用的齒輪鋼進行了循環變形下的性能研究。Won 等對第三代齒輪的重載條件下的靜態拉伸性能進行了研究。Emami等研究了第三代齒輪的靜態強度和熱處理工藝等。Savic 等研究了 3GAHSS 這種汽車車用第三代鋼的使用情況。Chang 等研究了汽車車用第三代車用鋼的熱處理硬度層的剪切間隙對材料斷裂的影響。綜上所述,針對第三代航空用齒輪鋼的彎曲疲勞性能的研究還比較少,目前還未見第三代齒輪鋼彎曲疲勞極限及 R?S?N 曲線結果。
本文針對 15Cr14Co12Mo5Ni2WA 鋼(第三代航空齒輪鋼)材料的齒輪的彎曲疲勞性能進行研究,通過對比第三代航空齒輪鋼和第一代航空齒輪鋼的性能差距,給出其在航空齒輪設計中的指導數值。本文確定了該材料的試驗方案、夾具參數及數據處理方法,對該材料圓柱齒輪輪齒進行了彎曲疲勞試驗,依據試驗結果得到壽命經驗分布函數,按對數正態分布、二參數威布爾分布對數據進行了擬合,得到了齒輪材料彎曲疲勞極限及 R ?S?N 曲線,并比較分析了第一代齒輪鋼和第三代齒輪鋼輪齒的疲勞性能差異。
一、彎曲疲勞強度試驗方法
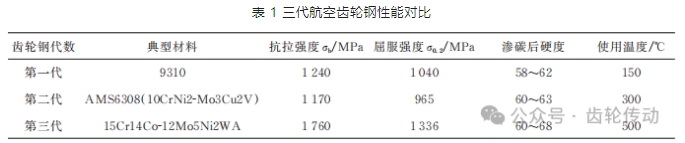
試驗齒輪設計:常溫下第一、二、三代航空齒輪鋼的靜力學性能如表 1 所示,由表可知,第三代齒輪鋼在抗拉強度、屈服強度、滲碳后硬度和使用溫度方面都得到了較大的提升,但其疲勞特性未知需要進一步研究。
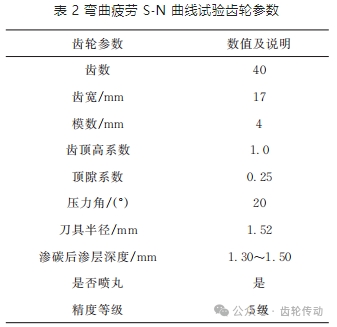
GB/T 14230?93《齒輪彎曲疲勞強度試驗方法》對齒輪的彎曲疲勞方法進行了詳細的規定,本文采用標準規定的齒輪脈動加載試驗法(B 試驗法)進行第三代齒輪鋼齒輪的彎曲疲勞強研究,根據標準規定的試驗齒輪參數和精度,設計試驗齒輪參數如表 2 所示。
試驗方法:采用“B 試驗法”進行試驗時,需要參考標準 GB/T 14230?1993 設計脈動疲勞試驗機上專用齒輪試驗夾具,國標中夾具設計計算的跨齒數 n 和載荷作用點壓力角 αE 的計算存在問題,本文對其計算公式進行修正,具體計算公式如下:
國標給出的計算跨齒數 n為
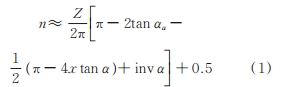
式中 Z 為齒數,αa為齒頂壓力角,x 為變位系數,α 為分度圓壓力角,inv(·)為漸開線函數。
國標給出的載荷作用點 E 點的壓力角 αE
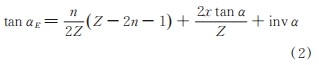
本文采用文獻給出的計算跨齒數 n 為
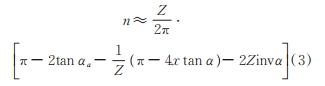
修正文獻給出作用點 E 點壓力角 αE
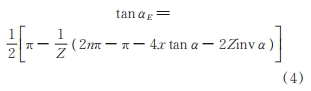
根據試驗齒輪的參數計算夾具參數如表 3 所示,夾具的具體設計尺寸如圖 1 所示。
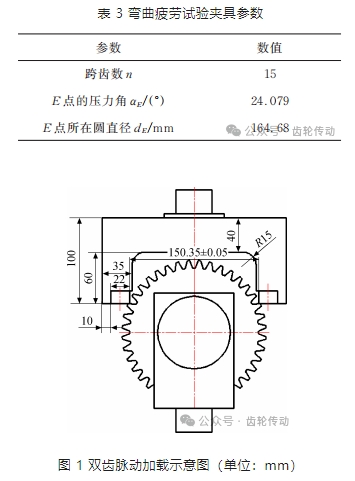
使用脈動疲勞試驗機對試驗齒輪的雙齒,同時進行脈動加載,直至輪齒出現彎曲疲勞失效或越出。試驗終止并獲得輪齒在試驗應力下的一個壽命數據。試驗中,脈動載荷僅施加在試驗輪齒對稱的單個輪齒上,試驗齒輪不做嚙合運轉,為了減小試驗輪齒對相鄰輪齒的壽命影響,試驗過程中所選取的試驗輪齒,與加過載荷的輪齒(包括支承齒)至少應間隔一個輪齒。
使用脈動疲勞試驗機加載試驗采用的應力比為 R=0.05,齒輪實際運行過程中的應力比為 R= 0,因此脈動循環齒根應力需要轉化,具體轉化方法見 GB/T 14230?1993 規定所示。
1)疲勞極限應力測試
齒輪彎曲壽命的無限壽命區,采用升降法測試疲勞極限應力。試驗時指定“循環基數 N0”(根據 GB3480 規定,本文采用 N0=3×106 次作為循環基數)下測定“疲勞極限”,若輪齒發生破壞并逐漸降低應力水平。試件在第 i 級最大應力 Si 作用下未達到循環基數 N0發生破壞,而在較低的第 i+1 級最大應力 Si+1作用下“越出”(達到循環基數未破壞),對應循環基數 N0的疲勞極限必發生在 Si和 Si+1之間。本試驗固定應力水平升降區間(即增量或減量)為 20~25 MPa。
2)R?S?N 曲線測定
齒輪有限壽命區采用常規成組法測定試驗齒輪的 R?S?N 曲線。試驗時取若干個應力水平進行試驗。最高應力級中的各試驗點的彎曲應力循環次數應不低于 0.5×105 次,最高應力級與次高應力級的應力間隔為總試驗應力范圍的 40%~ 50%,隨著應力降低,應力間隔逐漸減小,最低應力級中至少有一個試驗點越出。
3)試驗終止條件
試驗中若出現下列情況之一,均應判為失效:
(1)齒輪齒根出現可見疲勞裂紋。
(2)載荷或頻率下降 5%~10%。
(3)沿齒根斷齒。
試驗數據處理方法:由于齒輪的疲勞壽命和疲勞強度具有隨機現象,而隨機現象的數量規律一般只能根據數量有限的樣本觀測值來估計。
1)壽命經驗分布函數計算
齒輪彎曲疲勞試驗,采用雙齒加載形式試驗的數據處理方法進行處理 ,其失效順序用平均順序法計算,當對 P 對輪齒加載時,有 r 個齒失效(r≤P)。取 n=2P,壽命經驗分布函數值應按下式計算:
式中 nb 為試驗輪齒總數,Ai為試驗點壽命數值由小到大排列的平均順序。
式中 i為失效試驗點單獨排列的順序。
在未知試驗齒輪的壽命分布函數時,一般采用對數正態分布或二參數威布爾分布進行分布檢驗,確定分布類型,兩種分布函數分別為
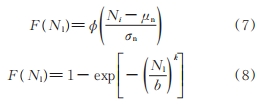
式中 Nl齒根應力循環次數;μn 為對數分布函數母體對數平均值;σn 為對數分布函數母體對數標準差;b 為威布爾分布函數的尺度參數;k 為威布爾分布函數的形狀參數。
2)壽命分布函數的擬合與檢驗
采用最小二乘法進行壽命分布的擬合優度檢驗,其具體步驟如下:
(1)通過壽命經驗分布函數計算得到 F (Nli)。
(2)分布函數的擬合。按對數正態分布擬合時,擬合公式為
按二參數威布爾分布擬合時,擬合公式為
3)R?S?N 曲線參數的確定
(1)按確定的壽命分布函數計算不同可靠度 R 的壽命值。對于對數正態分布,其計算公式為
對于二參數威布爾分布,其計算公式為
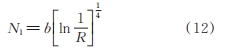
(2)擬合 R?S?N 曲線
齒輪彎曲疲勞曲線傾斜段方程(對數坐標中為直線方程)的形式為
式中 σf 為對應的 Nl 壽命下疲勞極限;m 為方程指數;C 為方程常數。
以各應力級相同可靠度的應力?壽命作為子樣,按上述公式用最小二乘法擬合,可以得到一系列不同可靠度的 S?N 曲線,即 R?S?N 曲線。
值得注意的是在低應力級下有壽命越出點,則高可靠度 S?N 曲線通常會失真,此時應根據相關系數剔除異常數據,依靠其余可靠度的 S?N 曲線來確定特定壽命級下的極限彎曲應力。
二、彎曲疲勞試驗及分析
根據上述疲勞強度的測試方案,對加工的 5 組試驗齒輪的彎曲疲勞強度進行測試,試驗加載過程見圖 2,試驗完成后的齒輪和斷齒如圖 3 所示。
為了得到真實的數據,每個應力等級的試驗樣本來自 5 個試驗齒輪,即在每個試驗齒輪上進行各個應力等級的試驗,保證每個應力等級的試驗樣本數據的來自不同的齒輪。
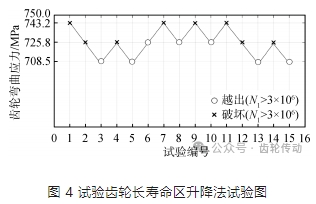
彎曲疲勞試驗數據:齒輪的無限壽命區采用升降試驗法進行測試,試驗齒輪升降試驗結果如圖 4 所示。有限壽命區用恒定應力水平試驗法獲得 3 個應力水平失效壽命見表 4 所示,每個應力水平測量 5 個點。
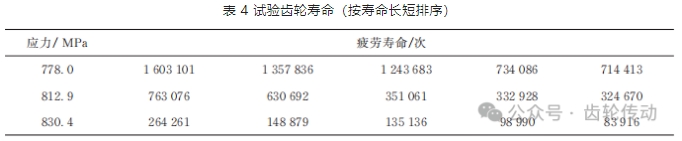
彎曲疲勞極限分析:無限壽命區的試驗數據采用對數正態分布、二參數威布爾分布方法進行擬合得到齒輪的在不同可靠度下的彎曲疲勞極限。95% 置信度下,采用對數正態分布擬合時疲勞極限如表 5 所示,其相關系數 r=0.837 7;95% 置信度下,采用二參數威布爾分布時其疲勞極限如表 6 所示,其相關系數 r=0.803 1。經過分析可以得到在 99% 的可靠度下第三代齒輪鋼的無限壽命區的應力采用對數正態分布擬合時已經達到了 687.6 MPa,采用二參數威布爾分布擬合時達到 673.4 MPa,基于二參數威布爾分布得到的齒輪疲勞極限更保守。
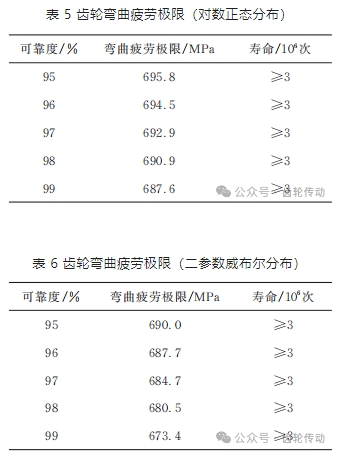
根據本單位前期第一代齒輪鋼(9310)鋼試驗結果,第一代齒輪鋼采用對數正態分布擬合時的齒輪彎曲疲勞極限 602 MPa,第三代航空齒輪鋼齒輪的應力水平提高了 14.2%,提高了航空齒輪傳動系統的可靠性。
彎曲疲勞壽命 R?S?N 曲線擬合:對有限壽命區的試驗結果表 4 進行數據分析,95% 置信度下,采用對數正態分布和二參數威布爾分布進行擬合,分析在置信度為 95% 下的不同可靠度的 R ?S?N 曲線,最終得到第三代齒輪鋼齒輪的 R?S?N 曲線。
基于對數正態分布擬合分析
1)壽命分布函數擬合
試驗齒輪的壽命(循環次數)與可靠度的之間的數據如表 7 所示,相關系數為 r92%=0.914 4;r96%=0.953 1;r98%=0.933 4。
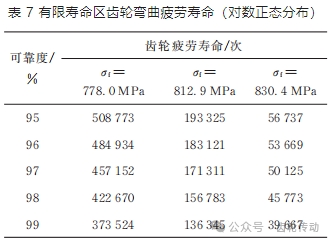
2)彎曲疲勞壽命 R?S?N 曲線擬合
95% 置信度下,對有限壽命區載荷下的齒輪彎曲疲勞數據進行 S?N 曲線方程擬合,擬合參數結果如表 8 所示,R ?S?N 曲線見圖 5 所示,根據擬合的曲線可得到,在可靠度為 99% 時該材料的彎曲疲勞極限為 696.7 MPa,與采用升降法得到的疲勞極限 687.6 MPa 誤差較小,S ?N 曲線可信度較高。第一代齒輪鋼的 S ?N 曲線如圖 6 所示(本單位前期試驗結果)。由圖 5 和圖 6 可知,第三代齒輪鋼在有限壽命區的許用應力要高于,在相同的載荷下,第三代齒輪鋼齒輪具有更高的壽命,更輕的質量,具有突出的優勢。
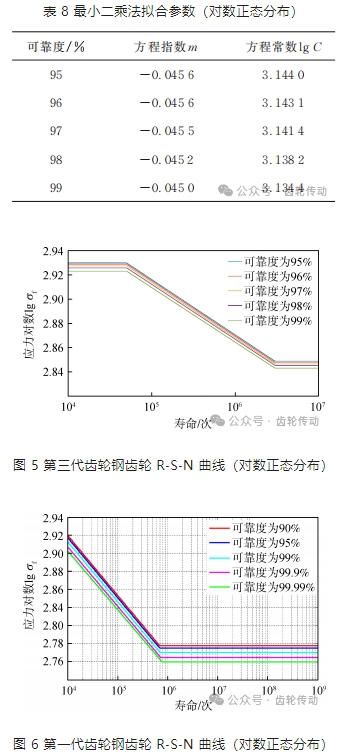
基于二參數威布爾分布的擬合分析
1)壽命分布函數擬合
95% 置信度下,基于二參數威布爾分布擬合,試驗齒輪的壽命(循環次數)與可靠度的之間的數據如表 9 所示,相關系數為r92%=0.936 4;r96%=0.865 4;r98%=0.940 5。
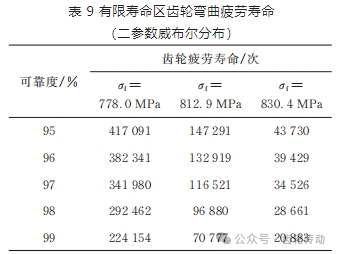
2)彎曲疲勞壽命 R?S?N 曲線擬合
95% 置信度下,基于二參數威布爾分布擬合試驗齒輪彎曲疲勞曲線方程參數和擬合曲線的疲勞極限結果如表 10 所示,R?S?N 曲線見圖 7 所示,根據擬合的曲線可得到,在可靠度為 R=99% 時該材料的彎曲疲勞極限為 681.5 MPa,與采用升降法得到的疲勞極限 673.4 MPa 誤差較小,S ?N 曲線可信度較高。第一代齒輪鋼的 S?N 曲線如圖 8 所示(本單位前期試驗結果)。
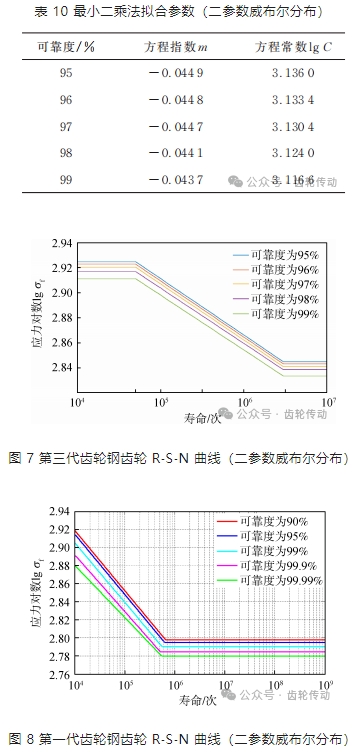
由圖 7 和圖 8 的比較結果與由圖 5 和圖 6 的結果相同,再次表明第三代齒輪鋼在彎曲強度方面具有較大的優勢。
采用對數正態分布擬合和二參數威布爾分布的擬合的 R?S?N 曲線得到的彎曲疲勞極限與升降法的到極限數值差距較小,同時驗證了擬合曲線的準確性和可靠性。
三、結論
本文以第三代航空齒輪鋼圓柱齒輪彎曲疲勞性能作為研究對象,根據國標 GB/T 14230?1993 制定了試驗方案,對國標的夾具計算存在的缺陷進行了修正,設計了試驗齒輪和專用夾具,采用“B 試驗法”開展了第三代齒輪鋼齒輪彎曲疲勞試驗,進行了試驗數據處理,得到了第三代齒輪鋼齒輪彎曲應力疲勞極限和不同可靠度下的結果。
1)完善了國標 GB/T 14230?1993 的“B 試驗法”專用夾具的跨齒數和載荷作用點的壓力角的計算公式,設計了脈動疲勞試驗機齒輪試驗專用的齒輪和夾具。
2)采用對數正態分布、二參數威布爾分布數據處理方法,對長壽命區的試驗數據進行了分析,試驗齒輪在可靠度為 99% 時,基于對數正態分布擬合齒輪齒根彎曲疲勞極限應力是 687.6 MPa,基于二參數威布爾分布齒輪齒根彎曲疲勞極限應力是 673.4 MPa;基于二參數威布爾分布得到的齒輪疲勞極限更保守。
3)在短壽命區內,第三代齒輪鋼試驗齒輪在可靠度為 99% 時,基于對數正態分布 S 曲線方程指數 m=-0.045 0,方程常數 lg C=3.134 4;基于兩參數威布爾分布方程指數 m=-0.043 7,方程常數 lg C=3.116 6,對數正態分布、二參數威布爾分布兩個方法擬合公式兩者差異較小。同時擬合曲線的上的彎曲疲勞極限數值與采用升降法的數值誤差較小,同時驗證了擬合曲線的準確性和可靠性。
4)第三代齒輪鋼齒輪在長壽命區齒輪齒根彎曲疲勞極限應力較第一代齒輪鋼齒輪提高了 14.2%;在短壽命區內相同在循環次數下其許用應力有較大提高;與第一代齒輪鋼相比第三代齒輪鋼在航空齒輪傳動方面具有較大的優勢。
參考文獻略.
