齒輪鬼頻是指嚙合特征頻率的非整數倍頻率,是由于齒輪齒面在加工異常時產生的振紋引起的。磨珩齒金剛輪的磨損,機床主軸的竄動,刀夾具的剛性及切削參數是否合理等都會引起該問題,如果生產過程中監控不及時,鬼頻批量出現會涉及大批售后問題,損失嚴重。但目前常用的齒輪精度檢測方法難以對其識別,因為波紋的振幅基本在 1 μm 以下,新的齒面波紋檢測手段非常必要。在相應的研究上 Matsumura 對單個齒形精度數據進行傅里葉分析發現,無法得到特征鬼頻。隨后采用最大熵譜分析法,對連續三個齒的精測數據進行計算,可以初步識別出鬼頻特征,但該方法需要對至少三個齒進行整個齒面的齒形精測,檢測及分析時間較長;Gravel 提出了一種用補償正弦函數法分析齒面波紋,將波紋中各諧波頻率依次用正弦函數擬合出來,能夠有效識別鬼頻,但文中并未提及具體算法。目前該方法已經集成到克林貝格的齒輪測量中心。Jonas建立了蝸桿磨的仿真模型,可以評估加工過程中齒面波紋的影響,為加工過程中實時控制波紋的產生打下了基礎。國內對波紋檢測及分析相關的研究較少,主要集中在問題改善上。根據齒輪嚙合原理結合傅里葉分析方法,提出了一種簡單快速識別齒面加工波紋的檢測手段,并結合實際案例驗證了有效性。
一、波紋度原理
從齒輪的嚙合過程可知,每個齒從嚙入到嚙出是沿著嚙合線傳動的,且為了保證各齒之間平滑過渡,在前一個齒嚙出時,后一個齒必須開始嚙入。這樣當齒輪旋轉一圈時,每個齒的嚙合線連接起來就形成了一條連續的直線。這條直線就是理想的剛性齒輪在空載狀態下的傳遞誤差曲線(圖 1)。針對這條連續曲線進行傅里葉分析即可得到振紋的特征頻率。按照傅里葉原理可知當每個齒在同樣的位置上有波紋時,如圖 1,圓形標記的位置,分解出來的都是倍頻。而波紋位置大于或小于嚙合線長度時,就會分解出鬼頻。
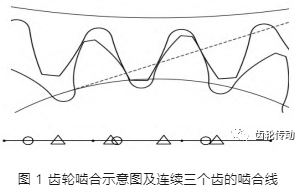
二、鬼頻識別步驟
每個齒的嚙合線數據可以通過齒輪測量中心獲取。由于齒輪參數及工件安裝角差異,產生的振紋與軸線夾角不同(圖 2)。如果振紋與軸線平行,則齒形方向的精測數據容易識別振紋,反之需要用齒向方向的數據。所以齒形和齒向方向的精度數據都需要檢測。下文以某 22 齒齒輪精測數據為例,利用 MATLAB 編程計算說明。
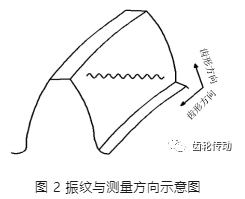
要獲得完整的特征曲線,首先需要對齒輪的所有齒進行精度檢測,并提取實際修形檢測數據,圖 3 展示了其中一條修形曲線數據。由于主要考慮加工引起的振紋問題,需要將數據中的設計修形量去除。從圖 3 中可以看出該齒輪采用的是拋物線鼓形及線性修形兩種方式,則可采用最小二乘法的二次曲線對理論修形量進行數據擬合。假設嚙合線長度和理論修形量的二次多項式為:
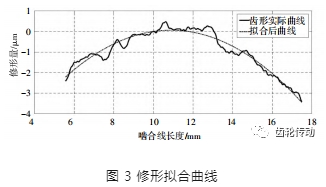
設實際的修形量為,基于最小二乘法原理考慮選取合適的使實際修形值和理論值偏差和最小:
按照式(2)的原則對圖 3 中的實際修形值采用 MATLAB 進行擬合,即可得到圖中虛線所示的理論修形量的二次曲線。然后用實際檢測值減去該理論值后就可獲得齒面的加工形狀,圖 4~5 即各個齒計算出來的齒形齒向波紋。可見齒形方向的波紋一致性比較好,按照上文理論,應該不存在鬼頻。齒向方向的波紋局部存在相位差,可能有鬼頻產生。
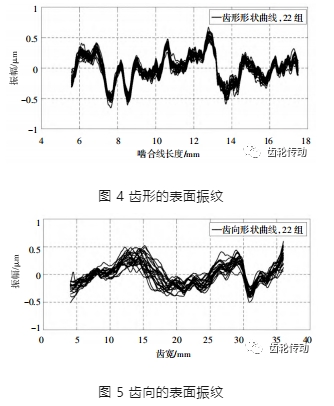
將齒形及齒向的精測數據按照嚙合線的方式分別組合起來,由于重合度的影響,每個齒之間的數據有重疊的部分,根據傳遞誤差的原理可知,重疊部分取其外包絡線,加上不重疊部分的曲線就分別構成了齒形齒向方向下空載的傳遞誤差曲線,圖 6 展示了其中三個齒連成一條曲線的狀態。
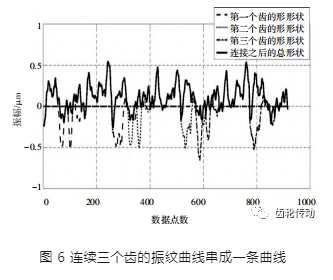
串接好的曲線是一條包含齒面振紋的不規則曲線,要提取其中的頻率特征,可采用傅里葉變換將其分解成一系列的簡諧信號:

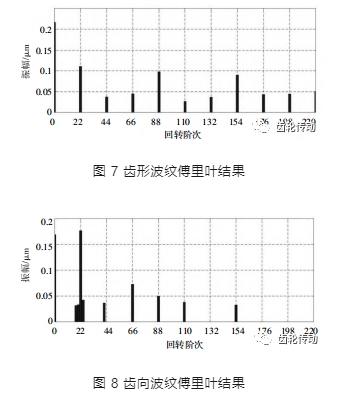
示,其中齒形上不存在倍頻以外的鬼頻。齒向在 22 階基頻附近有鬼頻存在,與上述預測對應,齒形齒向曲線有相位差時,需注意鬼頻的發生。
三、實例
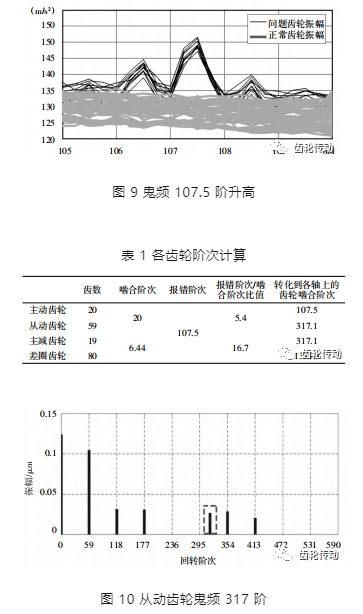
某款減速器在 EOL 交檢過程中批量發生 107.5 階振動頻率異常升高現象,如圖 9 所示。經計算發現報錯階次與齒輪嚙合階次的比值不為整數,初步判斷 107.5 階為齒輪鬼頻階次。接下來需要定位鬼頻所在齒輪,將 107.5 階分別以各輪所在軸為基準按速比計 算齒輪階次,各齒輪階次計算見表 1。對各齒輪進行齒形齒向精測,將數據依據上文的方法整理后進行傅里葉分析,結果在從動齒輪上發現 317 階振紋階次(圖 10),與表 1 階次對應,進一步確定 107.5 鬼頻可能來源于從動齒輪。后經 ABA 驗證,更換合格箱中的從動齒輪后,107.5 階鬼頻消失,振幅恢復到圖 9 中的灰線水平。
四、結語
齒面加工的異常波紋會導致嚴重的鬼頻和倍頻。基于外圓波紋度及齒輪嚙合的原理,提出一種簡單有效的識別方法,并分析發現當各齒精測數據一致時,基本不會發生鬼頻。當各齒數據有相位差時,有鬼頻風險。該方法可用在生產階段進行樣件抽檢,如果存在異常階次可及時調整加工參數。
參考文獻略.
